La onda de presión que se genera en una explosión de un depósito o en una BLEVE, provoca la formación de un cierto número de fragmentos (partes del propio depósito, valvulería, conexiones, etc.) con una energía cinética, a los que se denomina proyectiles o misiles, que pueden ser desplazados a distancias verdaderamente significativas. La estimación de este tipo de consecuencias, es un problema cuya solución no es nada fácil ya que depende de la energía de la explosión, de la trayectoria y de la distancia que alcanzan, problemas todos ellos de difícil determinación.
Una aproximación a la solución de este tipo de problema, parte de la energía que se genera en una explosión física o química, o bien procedente de una BLEVE. Parte de esta energía total forma ondas de presión y parte (Ef) transporta los fragmentos a determinadas distancias.
Hipótesis y limitaciones
El cálculo se lleva a cabo teniendo en cuenta que no existe rozamiento con el aire, con lo que el efecto es el más desfavorable posible. De la misma manera, el ángulo inicial de cálculo que se usará será el de 45º, es decir, el ángulo en virtud del cual la distancia alcanzada será la máxima.
Datos necesarios
Se necesitarán el peso total del depósito que se va a destruir, el número de fragmentos en los que se despedazará éste, la energía disponible para proyectiles y la altura a la que se encuentra el depósito desde el suelo.
Descripción
La energía disponible para la proyección de fragmentos, Ef es una fracción de la energía total y constituye la energía cinética de los fragmentos. Cualquier fragmento tendrá, por tanto la siguiente velocidad:
![]()
- Mr: masa total del recipiente (kg).
Para el cálculo de la velocidad en función de la distancia r, se utiliza la siguiente relación:
![]()
- Cw: coeficiente aerodinámico del fragmento (adimensional)
- Af: superficie del fragmento perpendicular a la trayectoria (m2)
- r: densidad del aire (kg/m3)
- Mf: Masa del fragmento (kg)
- Af: superficie del fragmento perpendicular a la trayectoria (m2)
Indicando con h la altura del lanzamiento del fragmento considerando un tiempo de vuelo:
El modelo calcula la máxima distancia de alcance rm a través de la siguiente iteracción:
![]()
El número de fragmentos se puede determinar a partir de la siguiente expresión:
Nº fragmentos = -3,77 + 0,0096 V
- V: volumen del depósito (m3)
Válido para depósitos comprendidos entre 700 y 2.500 m3.
En la imagen siguiente se presenta el rango de distribución de proyectiles en función de la distancia normalizada al número de radios de la bola de fuego para diversos casos (Ref: A. M. Birk, P. Eng. - BLEVE Research. Normalized projectile ranges for propane BLEVEs. Queen´s University at Kingstom).
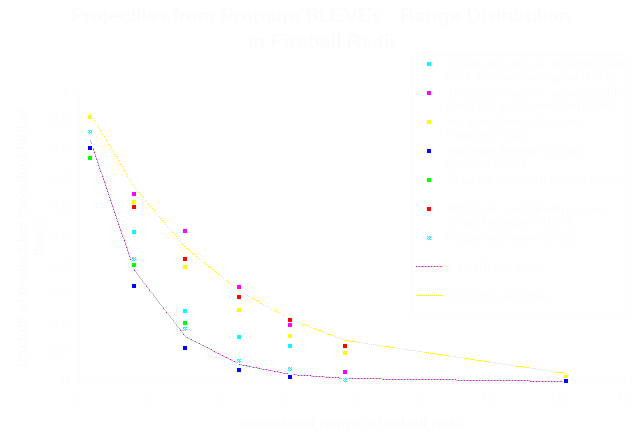
Distribución de proyectiles en función de la distancia